Intersezione Tra Spazi Vettoriali
Spazi Vettoriali Schema Riassuntivo Degli Spazi Vettoriali Docsity
Unione Intersezione E Somma Di Sottospazi
Esercizi Svolti Algebra Lineare E Geometria Docsity
La Somma Diretta Di Sottospazi Vettoriali Andrea Minini
Intersezione Tra Sfera E Paraboloide Imathematica
Ennio De Giorgi Selected Papers Pdf Free Download
Http Localwww Math Unipd It Candiler Didafiles Pdf Files Vect Sp Pdf
Notiamo che si ha.
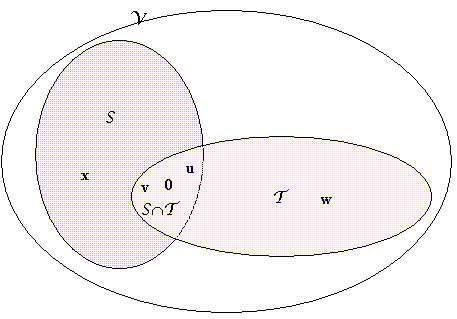
Intersezione tra spazi vettoriali. In quest video vengono spiegati i concetti di sottospazio intersezionedi sottospazio somma e viene spiegara la nota formula di grassmanntutto condito con opportuni esempi. Osserviamo che di minori siatti non ve ne e piu di uno. Osserviamo che di minori siatti non ve ne e piu di uno. Una base che appartenga allintersezione tra due sottospazi e una base che considerati v e w insiemi si trova proprio nellintersezione tra i due insiemi.
Definiamo poi l intersezione dei due sottospazi vettoriali e la chiamiamo lintersezione tra i due insiemi lasciamo a voi il compito di dimostrare che la somma e lintersezione tra due sottospazi sono a loro volta sottospazi vettoriali di. Quindi prendo un generico vettore di w 1. Lintersezione di due sottospazi vettoriali soddisfa la proprieta della somma degli spazi vettoriali. Lintersezione di w 1 w 2 contiene sicuramente una parte dei vettori di w 1.
Per riuscire nel vostro intento create un vettore generico v in grado di appartenere sia a v che a w. Quindi tale base deve appartenere sia a v che a w. Proprieta 2 prodotto per verificare la seconda proprieta dei sottospazi prendo uno scalare k e un elemento generico x di xy. Dimv w 4rangoa.
Non solo quelle di w 1. Alcuni esercizi di riepilogo sulla somma e lintersezione di sottospazi vettoriali e sulla formula di grassmann si tratta di esercizi simili a quelli trad. Intersezione e somma di sottospazi vettoriali 59 nota 64 nellesempio precedente abbiamo trovato una base di v w cercando un minore di ordine 3 invertibile. Unaltra base di v w e data quindi dagli ultimi tre vettori.
Per esempio anche il minore formato dalle prime tre righe e dalle ultime tre colonne e invertibile. Da questo deduco che i vettori di w 1 che si trovano nellintersezione w 1 w 2 devono rispettare anche le proprieta del sottospazio w 2. Px tp 1xtp 2x t22xx2 5x4 ed una sua base e data dal vettore 22xx2 5x4. Basta usare il teorema di caratterizzazione cosi come spiegato nella lezione come stabilire se un insieme e un sottospazio vettoriale.
